Manohara
ww-robinie
eigentlich dachte ich, die Aufgabe sei gut lösbar.
Jetzt habe ich eine ersten Versuch gemacht und blicke deutlich weniger durch als vorher.
Die Ecke soll durch 3 Schrauben gehalten werden, die jeweils senkrecht durch das Bein - bzw. die Zarge - in eine Kugel führen.
In der Kugel sind 3 Löcher, die alle auf die Mitte zeigen und jeweils 90° zueinander stehen.
Die 3 Hölzer sind in 45° so abgesägt und passen - ohne die Schrauben - mit der Kugel, perfekt zusammen.
Was überhaupt nicht passt, sind die Schrauben (die hier die verkehrte Länge haben, weil ich momentan keine passenden da habe)
Wenn die drin sind, stimmen weder die Winkel, noch die Längen.
Die Konstruktion mit Worten so zu beschreiben, wie sie sein soll finde ich schon nicht einfach. Nur mit Bildern zu machen.
Die Fehler (in den Winkeln, den Längen und der Einlass-Tiefe der Kugel) zu benennen, finde ich noch schwieriger und mögliche Lösungsvorschläge habe ich zwar, aber sie zu beschreiben ... ähhh.
Zum Bohren der Löcher im Holz und den Messing-Kugeln habe ich eine kleine Metall-Fräse, mit der man sehr genau Winkel einstellen und Bohrungen genau gleich widerholen kann.
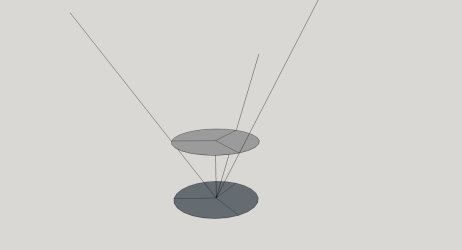
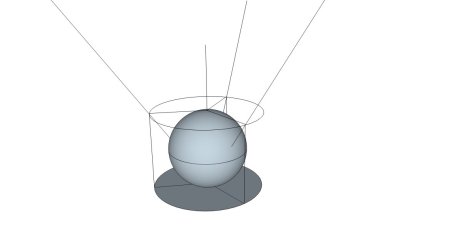
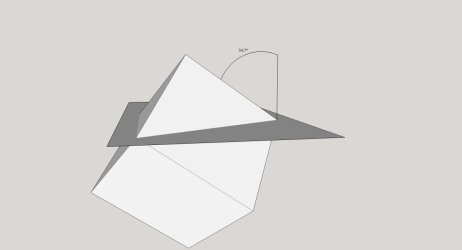
Auf den letzten 3 Bildern sieht man, wie es gemeint ist.
Innen sitzt die Kugel, auf der Außenseite sitzen Schraubenköpfe mit - an das Holz angepasste - Metall-Unterlegscheiben (die gibt's noch nicht).
Wenn die Gewindelöcher in der Kugel im richtigen Winkel am richtigen Fleck sind, müsste eigentlich alles so sein wie gedacht.
Da sind die 3 Bohrungen, die in 90° zueinander stehen und sich in der Mitte der Kugel treffen.
Wieso das nicht geklappt hat, ist mir ein Rätsel und ich bin gespannt, welche Überlegungen Ihr dazu habt.
Das Ganze entsteht für einen Beistelltisch aus Pock-Holz, was sich schlecht bis garnicht leimen lässt, weswegen ich mir diese Metall-Verbindung ausdenke, die auch den Vorteil hat, dass sie sich nachziehen - und - falls gewünscht - wieder zerlegen lässt.
... ich bin echt überrascht, welche Probleme da auftauchen.
Jetzt habe ich eine ersten Versuch gemacht und blicke deutlich weniger durch als vorher.
Die Ecke soll durch 3 Schrauben gehalten werden, die jeweils senkrecht durch das Bein - bzw. die Zarge - in eine Kugel führen.
In der Kugel sind 3 Löcher, die alle auf die Mitte zeigen und jeweils 90° zueinander stehen.
Die 3 Hölzer sind in 45° so abgesägt und passen - ohne die Schrauben - mit der Kugel, perfekt zusammen.
Was überhaupt nicht passt, sind die Schrauben (die hier die verkehrte Länge haben, weil ich momentan keine passenden da habe)
Wenn die drin sind, stimmen weder die Winkel, noch die Längen.
Die Konstruktion mit Worten so zu beschreiben, wie sie sein soll finde ich schon nicht einfach. Nur mit Bildern zu machen.
Die Fehler (in den Winkeln, den Längen und der Einlass-Tiefe der Kugel) zu benennen, finde ich noch schwieriger und mögliche Lösungsvorschläge habe ich zwar, aber sie zu beschreiben ... ähhh.
Zum Bohren der Löcher im Holz und den Messing-Kugeln habe ich eine kleine Metall-Fräse, mit der man sehr genau Winkel einstellen und Bohrungen genau gleich widerholen kann.
Auf den letzten 3 Bildern sieht man, wie es gemeint ist.
Innen sitzt die Kugel, auf der Außenseite sitzen Schraubenköpfe mit - an das Holz angepasste - Metall-Unterlegscheiben (die gibt's noch nicht).
Wenn die Gewindelöcher in der Kugel im richtigen Winkel am richtigen Fleck sind, müsste eigentlich alles so sein wie gedacht.
Da sind die 3 Bohrungen, die in 90° zueinander stehen und sich in der Mitte der Kugel treffen.
Wieso das nicht geklappt hat, ist mir ein Rätsel und ich bin gespannt, welche Überlegungen Ihr dazu habt.
Das Ganze entsteht für einen Beistelltisch aus Pock-Holz, was sich schlecht bis garnicht leimen lässt, weswegen ich mir diese Metall-Verbindung ausdenke, die auch den Vorteil hat, dass sie sich nachziehen - und - falls gewünscht - wieder zerlegen lässt.
... ich bin echt überrascht, welche Probleme da auftauchen.
Anhänge
Zuletzt bearbeitet:











![IMG_1682[1].JPG](/forum/data/attachments/192/192032-59dcbbccf6589bb6bf68a2d2d28c2f2b.jpg)
![IMG_E1683[1].JPG](/forum/data/attachments/192/192033-c0de9e559f924145819ce09da6f806cd.jpg)
![IMG_E1684[1].JPG](/forum/data/attachments/192/192034-3c9f115372f5acacfb302f0666bc0fe8.jpg)


