Du verwendest einen veralteten Browser. Es ist möglich, dass diese oder andere Websites nicht korrekt angezeigt werden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
raziausdud
ww-robinie
Hallo Uli,
gute Idee und schöne Zeichnung. Könntest Du ihm nicht - wenns keine große Mühe macht - gleich noch 1-2 weitere Versionen anbieten. Das Dach wird so recht flach und ich befürchte, dass es ihm nicht gefällt (weiter vorne hat er bei zwei gezeichneten Wahlmöglichkeiten von mir ein deutlich steileres gewünscht, geschätzte 30 Grad Neigung). Und ich befürchte, dann müssten wir noch mal von ganz vorn anfangen, weil Ralle immer nur Schritt für Schritt vorankommt. Ich würde zusätzlich einmal mit Spitzenwinkel 55 Grad und einmal mit 52 Grad vorschlagen, eventuell gar noch eine dritte Version mit 49 Grad. Wenn Du die Pyramidenschnitt-Tabelle zur Hand hast, mach es gern genauer, für 20, 25 und 30 Grad Dachneigung. Danke.
p.s. ich hab die Tabelle jetzt selbst gefunden, Spitzenwinkel für 20 Grad Dachneigung ist demnach 57 Grad, für 25 Grad sind es 55 Grad, für 30 Grad dann 53 Grad, immer rund. Ich musste ein wenig Rechnen und hoffe, dass sich kein Fehler eingeschlichen hat. Man wird hier irgendwann müde ...
Danke und Grüße
Rainer
gute Idee und schöne Zeichnung. Könntest Du ihm nicht - wenns keine große Mühe macht - gleich noch 1-2 weitere Versionen anbieten. Das Dach wird so recht flach und ich befürchte, dass es ihm nicht gefällt (weiter vorne hat er bei zwei gezeichneten Wahlmöglichkeiten von mir ein deutlich steileres gewünscht, geschätzte 30 Grad Neigung). Und ich befürchte, dann müssten wir noch mal von ganz vorn anfangen, weil Ralle immer nur Schritt für Schritt vorankommt. Ich würde zusätzlich einmal mit Spitzenwinkel 55 Grad und einmal mit 52 Grad vorschlagen, eventuell gar noch eine dritte Version mit 49 Grad. Wenn Du die Pyramidenschnitt-Tabelle zur Hand hast, mach es gern genauer, für 20, 25 und 30 Grad Dachneigung. Danke.
p.s. ich hab die Tabelle jetzt selbst gefunden, Spitzenwinkel für 20 Grad Dachneigung ist demnach 57 Grad, für 25 Grad sind es 55 Grad, für 30 Grad dann 53 Grad, immer rund. Ich musste ein wenig Rechnen und hoffe, dass sich kein Fehler eingeschlichen hat. Man wird hier irgendwann müde ...
Danke und Grüße
Rainer
Friederich
ww-robinie
- Registriert
- 14. Dezember 2014
- Beiträge
- 8.120
Ralle, hast du einen Zirkel?
Es ist einfacher du konstruierst damit dein Dreieck, dann brauchst du keine Winkel messen.
Erst die Grundlinie zeichnen mit 18,6cm, dann schlägst du um jedes Ende einen Kreisbögen mit 19,1 cm. Da wo sich die beiden Kreisbögen schneiden, ist dann die Spitze deines Dreiecks.
Das ist nicht nur einfacher, sondern auch viel präziser.
Es ist einfacher du konstruierst damit dein Dreieck, dann brauchst du keine Winkel messen.
Erst die Grundlinie zeichnen mit 18,6cm, dann schlägst du um jedes Ende einen Kreisbögen mit 19,1 cm. Da wo sich die beiden Kreisbögen schneiden, ist dann die Spitze deines Dreiecks.
Das ist nicht nur einfacher, sondern auch viel präziser.
falco
ww-robinie
Ich sehe schon kommen dass das Ganze auf 10 Seiten Thread endet.
60% sind erreicht und es gab doch eine Fülle an Möglichkeiten.
Ralle83
ww-esche
- Registriert
- 23. September 2016
- Beiträge
- 467
Zirkel habe ich keinen ich habe ja jetzt die mase irgenwie werde ich das auch hin bekommen .. nur das mit den 58 ° meist du doch so das ich einen Strich in 58 °machen muss . Dann einen grade runter richtig.
Und was meinst du mit 5 mm auf beiden Seiten abschneiden?
Und was meinst du mit 5 mm auf beiden Seiten abschneiden?
Time_to_wonder
ww-robinie
Und was meinst du mit 5 mm auf beiden Seiten abschneiden?
Im Anhang ein maßstäblich konstruiertes Detail. Das kannst Du 6x ausdrucken und ausschneiden (ach nee, Du hast ja keinen PC, oder?). Also das was Mark meint, ist das Abschneiden Deiner vorhandenen Dreiecke an den roten Linien.
Anhänge
Holzfummler
ww-robinie
@ralle 83,
nimm als Zirkelersatz eine entsprechend lange Leiste und durchbohre in den notwendigen Abständen 2mm Löcher. Mit entsprechendem Stift/Nagel kann du alles markieren/anreissen.
Ist ein einfacher Ersatz, funzt super und bei entsprechender Beschriftung eine immer wieder verwendbare Lehre für Serienfertigung.
Gruß
Thomas
nimm als Zirkelersatz eine entsprechend lange Leiste und durchbohre in den notwendigen Abständen 2mm Löcher. Mit entsprechendem Stift/Nagel kann du alles markieren/anreissen.
Ist ein einfacher Ersatz, funzt super und bei entsprechender Beschriftung eine immer wieder verwendbare Lehre für Serienfertigung.
Gruß
Thomas
Ralle83
ww-esche
- Registriert
- 23. September 2016
- Beiträge
- 467
Ja gut alles klar oder so .
Laptop habe ich schon nur halt kein Zeichen Programm..
Teluke ich habe denn Leuchtturm fertig es fehlt halt nur das Dach. Wenn dir das zu langweilig wirt dann geh doch einfach . Durch dein scheiss gelaber was keiner hören will werden die Seiten nur immer voller.
Laptop habe ich schon nur halt kein Zeichen Programm..
Teluke ich habe denn Leuchtturm fertig es fehlt halt nur das Dach. Wenn dir das zu langweilig wirt dann geh doch einfach . Durch dein scheiss gelaber was keiner hören will werden die Seiten nur immer voller.
Durch dein scheiss gelaber was keiner hören will werden die Seiten nur immer voller.
Dafür sorgst Du schon selbst dadurch dass Du nichts kapierst.
Wie viele Male musst du diese, wirklich einfache Sache, noch vorgebetet bekommen?
Außerdem hatte ich alle anderen angesprochen, Dich nicht.
Noch eine Kleinigkeit: "gelaber" schreibt man groß.
Hinter "gelaber und hinter will kommt außerdem jeweils noch ein Komma.
Sorry, musste sein.
Jonamu
ww-nussbaum
- Registriert
- 17. März 2014
- Beiträge
- 98
Hier ist das ganze auch noch einmal erklärt. http://math-it.org/Publikationen/Trichterzinkung.pdf
Dort ist auch eine Tabelle enthalten, die für die jeweiligen Winkelkombinationen die Schmiegenwerte angibt.
Bei deinem 6 Eck also 120° und 15° Dachneigung müssten deine Bretter untereinander 8,5° haben. Hiermit ist nicht das Dreieck gemeint!
Dort ist auch eine Tabelle enthalten, die für die jeweiligen Winkelkombinationen die Schmiegenwerte angibt.
Bei deinem 6 Eck also 120° und 15° Dachneigung müssten deine Bretter untereinander 8,5° haben. Hiermit ist nicht das Dreieck gemeint!
Time_to_wonder
ww-robinie
Hier ist das ganze auch noch einmal erklärt. http://math-it.org/Publikationen/Trichterzinkung.pdf
Dort ist auch eine Tabelle enthalten, die für die jeweiligen Winkelkombinationen die Schmiegenwerte angibt.
Bei deinem 6 Eck also 120° und 15° Dachneigung müssten deine Bretter untereinander 8,5° haben. Hiermit ist nicht das Dreieck gemeint!
Das verstehe noch nicht einmal ich.
Ich denke, es geht in diesem Thread nicht darum, wer den dollsten lateinischen Trigonometrie-Begriff auftut oder die komplizierteste Formel mit den meisten Wurzelzeichen ergoogelt, sondern wie man diesen komplexen Sachverhalt auf ein paar wenige Worte und Angaben reduziert. Anders kommen wir hier nicht weiter...
Time_to_wonder
ww-robinie
Dafür sorgst Du schon selbst dadurch dass Du nichts kapierst.
Ist das nötig?
Jörg - wir sind jetzt schon bei Schablonen zum Ausschneiden. Die nächste Stufe wäre hinfahren, messen und zuschneiden..
Oder ich zeichne noch ein paar Laschen dran, dann kann man es wie einen Miserior-Spendenkarton zusammenkleben.
Grüße
Uli
Oder ich zeichne noch ein paar Laschen dran, dann kann man es wie einen Miserior-Spendenkarton zusammenkleben.
Grüße
Uli
Wird euch das nicht zu langweilig?
Wenn der TE sich sein eigenes Projekt nicht räumlich vorstellen kann wird das eh nichts.
Es scheint wirklich an der räumlichen Vorstellung zu liegen oder noch anderen Dingen.
Ich hatte in #9 ein Video mit einem einfachen Beispiel verlinkt.
Weder zu diesem noch zu anderen Vorschlägen kam vom Fragesteller auch nur ansatzweise der Versuch etwas umzusetzen.
Nun bei #88 auch kein Fortschritt.
Irgendwie ist das traurig, trollig oder einfach nur ...
rorob
ww-robinie
Traurig ist, dass man nicht weiß, ob es traurig oder trollig ist.
Den TE beschäftigt ja ein Leuchtturm nicht erst seit diesem thread.
Gruß
Robert
Den TE beschäftigt ja ein Leuchtturm nicht erst seit diesem thread.
Gruß
Robert
raziausdud
ww-robinie
Man kann das benötigte Dreick auf zwei Weisen konstruieren/zeichnen:
a) entweder mit 2 Strecken und dem Winkel, den diese Strecken bilden. Vielleicht hilft Dir das Bild einer Schere: die Klingenlänge ist das eine, die Öffnung der Schere das andere (das wären hier die 57,3 Grad - oder hatten wir 58,3 Grad ... )
)
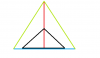
b) oder nur mit Strecken, nämlich der Höhe des Dreieck (siehe Skizze, rot) und der Basis (Querstrecke unten, blau). Dazu fällt mir am ehesten ein Zelt ein, dessen Höhe und dessen Boden bekannt und festgesetzt/bestimmt ist, die schrägen Seitenbahnen ergeben sich daraus sozusagen automatisch.
Hier b nochmal anhand der Skizze erklärt:
zuerst die rote Linie zeichnen, 16,7 cm lang. Am unteren Punkt der roten Linie legst Du die Kante des Geodreiecks (schwarz) an, die Mittellinie des Geodreiecks auf die rote Line und ziehst nach links eine Linie mit 9,3 cm und nach rechts eine Linie mit 9,3cm, die gesamte blaue Linie ist somit 18,6 cm lang. Wenn das Geodreieck nicht ausreicht, die Strecken gerade verlängern und bei 9,3cm markieren.
Nun die Endpunkte der blauen Linie mit dem Punkt oben der roten Linie verbinden, das sind die grünen Linien. Nun hast Du eines von den benötigten sechs Dreiecken.
Grad fällt mir ein ... Du hast ja offensichtlich für Deine Pappdreiecke Methode a) genommen. Ich könnt mir vorstellen, dass Du bei der Zeichenmethode a) mit Winkel auf dem Geodreick wegen der ..,3 noch mal drei Striche weitergehst. Das wäre falsch. Das wären volle drei Grad mehr als 57 Grad, nämlich 57 plus 3 = 60 Grad. Das würden erklären, dass Dein Pappsechseck flach auf dem Tisch liegt. Nimm einfach runde 57 Grad, das ist drei Striche vor 60 Grad. Leichter zu zeichnen und genauer ist mE aber Methode b laut Skizze.
Rainer
a) entweder mit 2 Strecken und dem Winkel, den diese Strecken bilden. Vielleicht hilft Dir das Bild einer Schere: die Klingenlänge ist das eine, die Öffnung der Schere das andere (das wären hier die 57,3 Grad - oder hatten wir 58,3 Grad ...
b) oder nur mit Strecken, nämlich der Höhe des Dreieck (siehe Skizze, rot) und der Basis (Querstrecke unten, blau). Dazu fällt mir am ehesten ein Zelt ein, dessen Höhe und dessen Boden bekannt und festgesetzt/bestimmt ist, die schrägen Seitenbahnen ergeben sich daraus sozusagen automatisch.
Hier b nochmal anhand der Skizze erklärt:
zuerst die rote Linie zeichnen, 16,7 cm lang. Am unteren Punkt der roten Linie legst Du die Kante des Geodreiecks (schwarz) an, die Mittellinie des Geodreiecks auf die rote Line und ziehst nach links eine Linie mit 9,3 cm und nach rechts eine Linie mit 9,3cm, die gesamte blaue Linie ist somit 18,6 cm lang. Wenn das Geodreieck nicht ausreicht, die Strecken gerade verlängern und bei 9,3cm markieren.
Nun die Endpunkte der blauen Linie mit dem Punkt oben der roten Linie verbinden, das sind die grünen Linien. Nun hast Du eines von den benötigten sechs Dreiecken.
Grad fällt mir ein ... Du hast ja offensichtlich für Deine Pappdreiecke Methode a) genommen. Ich könnt mir vorstellen, dass Du bei der Zeichenmethode a) mit Winkel auf dem Geodreick wegen der ..,3 noch mal drei Striche weitergehst. Das wäre falsch. Das wären volle drei Grad mehr als 57 Grad, nämlich 57 plus 3 = 60 Grad. Das würden erklären, dass Dein Pappsechseck flach auf dem Tisch liegt. Nimm einfach runde 57 Grad, das ist drei Striche vor 60 Grad. Leichter zu zeichnen und genauer ist mE aber Methode b laut Skizze.
Rainer
Anhänge
Ist das nötig?
Nein, ist es nicht.
Und ohne das "scheiss gelaber" hätte ich sowas auch nicht geschrieben.
Ralle83
ww-esche
- Registriert
- 23. September 2016
- Beiträge
- 467
Ich habe einen 58.3° Strich gemacht. dann einen graden Strich runter. Dann beide Seite auf 19.1 einen quar Streich gemacht. Und dann aus schneiden fertigMan kann das benötigte Dreick auf zwei Weisen konstruieren/zeichnen:
a) entweder mit 2 Strecken und dem Winkel, den diese Strecken bilden. Vielleicht hilft Dir das Bild einer Schere: die Klingenlänge ist das eine, die Öffnung der Schere das andere (das wären hier die 57,3 Grad - oder hatten wir 58,3 Grad ...)
b) oder nur mit Strecken, nämlich der Höhe des Dreieck (siehe Skizze, rot) und der Basis (Querstrecke unten, blau). Dazu fällt mir am ehesten ein Zelt ein, dessen Höhe und dessen Boden bekannt und festgesetzt/bestimmt ist, die schrägen Seitenbahnen ergeben sich daraus sozusagen automatisch.
Hier b nochmal anhand der Skizze erklärt:
zuerst die rote Linie zeichnen, 16,7 cm lang. Am unteren Punkt der roten Linie legst Du die Kante des Geodreiecks (schwarz) an, die Mittellinie des Geodreiecks auf die rote Line und ziehst nach links eine Linie mit 9,3 cm und nach rechts eine Linie mit 9,3cm, die gesamte blaue Linie ist somit 18,6 cm lang. Wenn das Geodreieck nicht ausreicht, die Strecken gerade verlängern und bei 9,3cm markieren.
Nun die Endpunkte der blauen Linie mit dem Punkt oben der roten Linie verbinden, das sind die grünen Linien. Nun hast Du eines von den benötigten sechs Dreiecken.
Grad fällt mir ein ... Du hast ja offensichtlich für Deine Pappdreiecke Methode a) genommen. Ich könnt mir vorstellen, dass Du bei der Zeichenmethode a) mit Winkel auf dem Geodreick wegen der ..,3 noch mal drei Striche weitergehst. Das wäre falsch. Das wären volle drei Grad mehr als 57 Grad, nämlich 57 plus 3 = 60 Grad. Das würden erklären, dass Dein Pappsechseck flach auf dem Tisch liegt. Nimm einfach runde 57 Grad, das ist drei Striche vor 60 Grad. Leichter zu zeichnen und genauer ist mE aber Methode b laut Skizze.
Rainer
Ralle83
ww-esche
- Registriert
- 23. September 2016
- Beiträge
- 467
Es scheint wirklich an der räumlichen Vorstellung zu liegen oder noch anderen Dingen.
Ich hatte in #9 ein Video mit einem einfachen Beispiel verlinkt.
Weder zu diesem noch zu anderen Vorschlägen kam vom Fragesteller auch nur ansatzweise der Versuch etwas umzusetzen.
Nun bei #88 auch kein Fortschritt.
Irgendwie ist das traurig, trollig oder einfach nur ...
Ich habe das Video angeschaut und auch geschrieben das er nicht erklärt wie er das Dreieck aufgezeichnet hat .
Fiamingu
ww-robinie
Doppelpost
Fiamingu
ww-robinie
Kann denn nicht jemand den Ralle zum
Basteln zu sich einladen?????? Dann geht das schneller....
Oder?????? Ich kann das nicht. Hab eh schon Bluthochdruck.
Ich kann das nicht. Hab eh schon Bluthochdruck.
Basteln zu sich einladen?????? Dann geht das schneller....
Oder??????