Diagonalbalken -Winkelberechnung?

[NewbieS]

Moin zusammen,

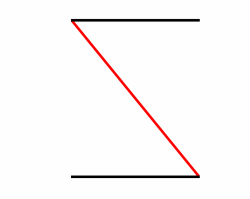
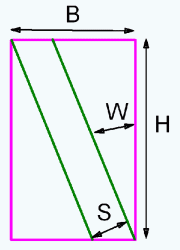
ich habe eine kleine, wahrscheinlich dumme Frage. Ich baue grade einen kleinen Dartschrank und "hänge" bei den Klappen. Ich habe dafür bisher einige Bretter mit zwei Querlatten verbunden. Zur weiteren Stabilisation möchte ich die beiden Latten mit einem dritten Brett in der Diagonalen verbinden (rote Linie in der angehängten Zeichnung). Aber wie genau berechne ich da den Winkel?! Alle bisherigen Versuche mit Anzeichnen erwiesen sich als zu ungenau. Vielleicht kennt ihr einen Trick?

Mir ist bewusst, dass da normalerweise ein Versatz in die Querlatten eingebaut wird. Darauf würde ich gerne verzichten, weil ich a) nicht das entsprechende Werkzeug habe und b) es sich "nur" um kleine Schranktüren handelt und nicht um eine massive Brettertür

 

[elmgi]

Eine Zeichnung kann ich nicht sehen, d.h. diese fehlt.

Mein Vorschlag:

Diagonalstrebe auflegen, anzeichnen und nur eine Seite sägen.
Gesägtes Brett wieder auflegen, anzeichnen und erneut - mit etwas Zugabe in der Länge - sägen.
Minimal nachsägen bei Bedarf.

 

[Hondo6566]

a^2 +b^2 = c^2
Winkel gibts dann aus dem Sinus-, Cosinus- oder Tangens-Satz.
Sollte man doch aus der Schule noch kennen.
Ansonsten gibt es im Internet zig Plattformen um ein rechtwinkliges Dreieck auszurechnen.
Gruß Andreas

 

[Friederich]

Diagonalstrebe auflegen, anzeichnen

Ja. Man kommt zwar nicht an die Unterseite um einen durchgehenden Strich anzuzeichnen, aber es gnügen ja in paar Millimeter an Anfang und Ende. Mit Lineal wird der Strich dann ganz durchgezogen.
Beim Sägen dann beachten, dass der Strich in ganzer Stärke stehenbleibt. Nicht so wie in den meisten anderen Fällen, in nur halber Stärke.

 

[Friederich]

Cosinus- oder Tangens-Satz.

Zuviel action.
Drauflegen und Anzeichnen ist mind. genauso genau.

 

[andama]

Guggst du: https://www.arndt-bruenner.de/mathe/scripts/Dreiecksberechnung.htm

 

[Hondo6566]

hier z.B.:
https://lmgtfy.com/?q=rechtwinkliges+dreieck+berechnen+online

 

[elmgi]

Und wenn die beiden erwähnten "Querlatten" nicht absolut präzise parallel verlaufen, dann hilft
in diesem Falle die Mathematik nur begrenzt weiter.

Auflegen und anzeichnen geht einfach und schnell, ohne jegliche Rechnerei.

 

[IngoS]

Hallo,

Zum Anzeichnen ist eine Schmiege ein gutes Hilfswerkzeug.

Rechnen ist bei so einer Aufgabe eher nicht angesagt, wie mehrere Andere hier schon angemerkt haben.

Gruß

Ingo

 

[Daniboy]

a^2 +b^2 = c^2
Winkel gibts dann aus dem Sinus-, Cosinus- oder Tangens-Satz.
Sollte man doch aus der Schule noch kennen....

Im ersten Moment ja, im Detail nein. Die Diagonal-Leiste hat ja eine gewisse Dicke.

Das macht es mathematisch eigentlich sehr aufwendig.
(Jedenfalls nicht einfach Pythagoras und Winkelfunktion).

 

[Hondo6566]

Die Diagonal-Leiste hat ja eine gewisse Dicke.

Und? Winkel bleibt winkel, die Latte kann noch so dick sein.

 

[Daniboy]

Und? Winkel bleibt winkel, die Latte kann noch so dick sein.

Nachtrag: Ja, aber es wäre nur dann so einfach wie du sagst, wenn die Stärke der Latte Null ist.

Mann muss ja den Diagonal-Lattenanschnitt abziehen um das Dreieck zu bekommen um mit den Winkelfunktionen weiterzurechnen.
Und dieser Latten-Anschnittswinkel ist ja genau in den Winkel den man noch nicht kennt. Und man kennt auch nicht die Länge dieser Schnittfläche, sondern nur die Lattenstärke.

 

[Hondo6566]

Zeig mir doch mal wo hier unterschiedliche Winkel sind:
(außer vieleicht 1-2 Grad zeichnerische Ungenauigkeit)

 

[Daniboy]

Dein linkes Bild entspricht für mich, dem des TE.
Ich meine, dass man es nur leicht berechnen kann, wenn diese Diagonale nur eine Linie ist. Wenn sie eine gewisse Dicke hat (egal wieviel) dann ist es rechnerisch schwierig.

Wie kann man also den Winkel "W" aus meiner Skizze berechen,
wenn H, B und S bekannt sind?

 

[Hondo6566]

Hallo,
der Winkel W entspricht identisch dem Winkel zur linken grünen Linie.
Und nur den Winkel wollte der Themenersteller in #1 wissen.
Gruß Andreas

PS: nennt sich übrigends Stufenwinkel. Da ist Alpha identisch mit Alpha Strich.
https://mathepedia.de/Stufen-_und_Wechselwinkel.html

 

[Daniboy]

Hallo,
der Winkel W entspricht identisch dem Winkel zur linken grünen Linie.
Und nur den Winkel wollte der Themenersteller in #1 wissen.
Gruß Andreas

PS: nennt sich übrigends Stufenwinkel. Da ist Alpha identisch mit Alpha Strich.
https://mathepedia.de/Stufen-_und_Wechselwinkel.html

Ja, das ist mir klar, aber wie berechnest du ihn aus den gegebenen Werten H, B und S?

 

[Friederich]

Im ersten Moment ja, im Detail nein. Die Diagonal-Leiste hat ja eine gewisse Dicke

Ah ja, stimmt ja. Aber du meinst wahrscheinlich "Breite"?.
Sogar auf CAD ist das nicht so ganz einfach zu zeichnen. edit: falls man einen vorher festgelegten Abstand zum Rand (kann auch Null sein)einhalten will.
Medium 5670 anzeigen

 

[Hondo6566]

wie berechnest du ihn aus den gegebenen Werten H, B

/edit/ falsch gelesen. Winkel aus Cosinus, Sinus oder Tangens. Standard in Hauptschule - oder?
Friedrich, die Diagonale kann auch im gleichen Winkel wie die rote Linie liegen - oder?
Es sieht natürlich schöner aus wenn die Brettkanten spitz zulaufen und nicht stumpf abgeschnitten werden.
Gruß Andreas

 

[Kaltregen]

Wie kann man also den Winkel "W" aus meiner Skizze berechen,
wenn H, B und S bekannt sind?

Hallo,

ich glaube ich habe eine Lösung des Rechenproblems.

Hier die Formel: W = ARCTAN ( B / H ) - ARCSIN ( S / WURZEL ( B² + H² ) )

Ich hab eine LibreOffice-Tabelle gemacht (Anhang) und die Werte mit denen im CAD bei mehreren unterschiedlichen Größen verglichen und es hat alles gepasst. Im Grund berechne ich erst den Winkel der echten Diagonalen der ganzen Fläche, berechne die Länge dieser und ziehe dann von dem Winkel den Winkel der Diagonalen im diagonalen Brett ab.

Gruß Michael

 

[hobbybohrer]

Hallo,
mit dem Taschenrechner ergibt sich aus den Werten für H, B und S und
den Hilfsgrößen C=H^2+B^2 und E=H^2-S^2
sin(alpha)=(B*S+(B^2*S^2+C*E)^0,5)/C.
Damit erhält man den Winkel alpha und aus dem obigen Ergebnis direkt
die Länge der Schnittlinie am Diagonalbrett: A=S/sin(alpha)
und die Länge des Diagonalbrettes L=(H^2-(B-S)^2)^0,5. ^0,5 heißt wie immer Wurzel aus...
Mit den angegebenen Zahlenwerten ist alpha=60,3°, A=23,02 und L=115,09.
Leider kann ich die Formeln hier nicht schöner darstellen.
Grüße Richard

 

[Frank73]

Und während Ihr noch rechnet, habe ich es schnell aufgelegt, abgezeichnet und abgesägt.
Fertsch.

 

[Kaltregen]

Aber wie genau berechne ich da den Winkel?! Alle bisherigen Versuche mit Anzeichnen erwiesen sich als zu ungenau.

Wenn er / sie das nicht geschrieben hätte, hätte ich es auch bei der Aussage "Anzeichnen und fertig" belassen

 

[blueball]

Ja, das ist mir klar, aber wie berechnest du ihn aus den gegebenen Werten H, B und S?

mittels Mathe .... Dein Winkel W ist der selbe wie unten wo eine Kathede dein S ist. Von dem kleine Dreieck also mit Winkel W und Kathede S die Hypothenuse ausrechnen und weiter geht's. Ganz einfach das Ganze. Rechnen ist aber hier nicht der praktikabelste Weg sondern anzeichnen und was schaffe

 

[Friederich]

Friedrich, die Diagonale kann auch im gleichen Winkel wie die rote Linie liegen - oder?

Kann man auch machen: Die Mittellinie des Brettes genau über die Diagonale und dann die Ecken abschneiden. Dann ist es ganz einfach zu berechnen.

 

[NewbieS]

Uh da habe ich ja doch eine größere Diskussion losgetreten. Der Tipp von @elmgi war Gold wert. Erst die eine Seite anzeichnen, sägen und dann die zweite Seite. Das sind so die kleinen Tricks, die einen Anfänger von einem erfahrenen Handwerker unterscheiden. Danke dafür!

Zu den ganzen mathematischen Lösungen: Ja, geht in der Theorie schon. Aber wie schon gesagt: Sobald da irgendwo eine minimale Abweichung drin ist, funktioniert das auch nicht mehr so richtig. Und da ich Anfänger bin, kalkuliere ich "menschliches Versagen" lieber mit ein