Hi zusammen
habe mir jetzt mal eine blaue Bosch Kapp und Zugsäge zugelegt, und gestern etwas herumgespielt.
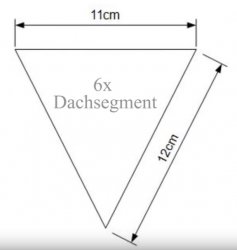
Bin da grad an einem neuen Vogelhäuschen drann und möchte oben einen 6 Eck Dach drauf machen, weil das Häuschen auch eine 6Eck Form hat.
Aber irgendwie komme ich nicht so richtig mit dem Dach zurecht.

Wenn ich das Dach dann auch 6 Teile aufteilen will, und dann natürlich ein leichtes Gefälle brauch muss ich ja auch die Seiten mit einer leichten Schräge Zuschneiden.
Wenn ich diese dann zusammen kleben will passt das letzte Teil einfach nicht,
obwohl alle Winkel eigentlich stimmig wären?????
Irgendwo habe ich einen Denkfehler
Vielleicht hatt jemand eine kleine Zeichnung wo ich mein Vorhaben ableiten kann.
Danke
Gruß Michael
Google-Ergebnis für http://picture.yatego.com/images/50ddb416dc9dc4.4/1422288667_vogelfutterhaus_6eck-kqh/holzwaren-wasmer-vogelhaus--6-eck-.jpg
habe mir jetzt mal eine blaue Bosch Kapp und Zugsäge zugelegt, und gestern etwas herumgespielt.
Bin da grad an einem neuen Vogelhäuschen drann und möchte oben einen 6 Eck Dach drauf machen, weil das Häuschen auch eine 6Eck Form hat.
Aber irgendwie komme ich nicht so richtig mit dem Dach zurecht.
Wenn ich das Dach dann auch 6 Teile aufteilen will, und dann natürlich ein leichtes Gefälle brauch muss ich ja auch die Seiten mit einer leichten Schräge Zuschneiden.
Wenn ich diese dann zusammen kleben will passt das letzte Teil einfach nicht,
obwohl alle Winkel eigentlich stimmig wären?????
Irgendwo habe ich einen Denkfehler
Vielleicht hatt jemand eine kleine Zeichnung wo ich mein Vorhaben ableiten kann.
Danke
Gruß Michael
Google-Ergebnis für http://picture.yatego.com/images/50ddb416dc9dc4.4/1422288667_vogelfutterhaus_6eck-kqh/holzwaren-wasmer-vogelhaus--6-eck-.jpg